142-Linked List Cycle II

Problem

Approach 1: Hash Table

Time complexity: O(n).

Space complexity: O(n).

Approach 2: Two Pointers: Floyd’s Tortoise and Hare

From 141, we know we can have one fast ptr, one slow ptr chase each other to detect cycle. Fast ptr moves two steps per time, slow ptr moves two step per time. When fast ptr meets slow ptr, we know there is a cycle, but we have no idea where the cycle begins.

Now consider the time point when fast ptr A first meets slow ptr B. The path B have gone through, path_B = non_cycle_path + cycle_path_B. The path A have gone through, path_A = non_cycle_path + cycle_path * N + cycle_path_B, where N is a positive integer. Also, path_A = 2 * path_B, so cycle_path * N = non_cycle_path + cycle_path_B, cycle_path * (N - 1) + (cycle_path - cycle_path_B) = non_cycle_path. Note that (cycle_path - cycle_path_B) is exactly the rest of the the current cycle for A to finish. If we reset B to the head of the list, and move A and B one step at a time together, after non_cycle_path step, both A (after finishing N cycles including the current one) and B will arrive at the begining of the cycle.

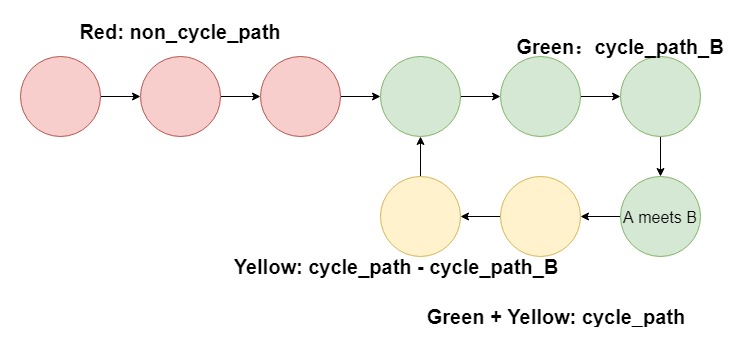
Time complexity: O(n).

Space complexity: O(1).

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;

        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;

            if (slow == fast) {
                slow = head;
                while (slow != fast) {
                    slow = slow->next;
                    fast = fast->next;
                }
                return slow;
            }
        }

        return nullptr;
    }
};