421-Maximum XOR of Two Numbers in an Array
Approach 1: Bitwise Trie
Use Bitwise Trie (a special trie where the alphabet is simply {0, 1}) to store binary prefixes in an efficient way. To maximize XOR, the strategy is to choose the opposite bit at each step whenever it’s possible.
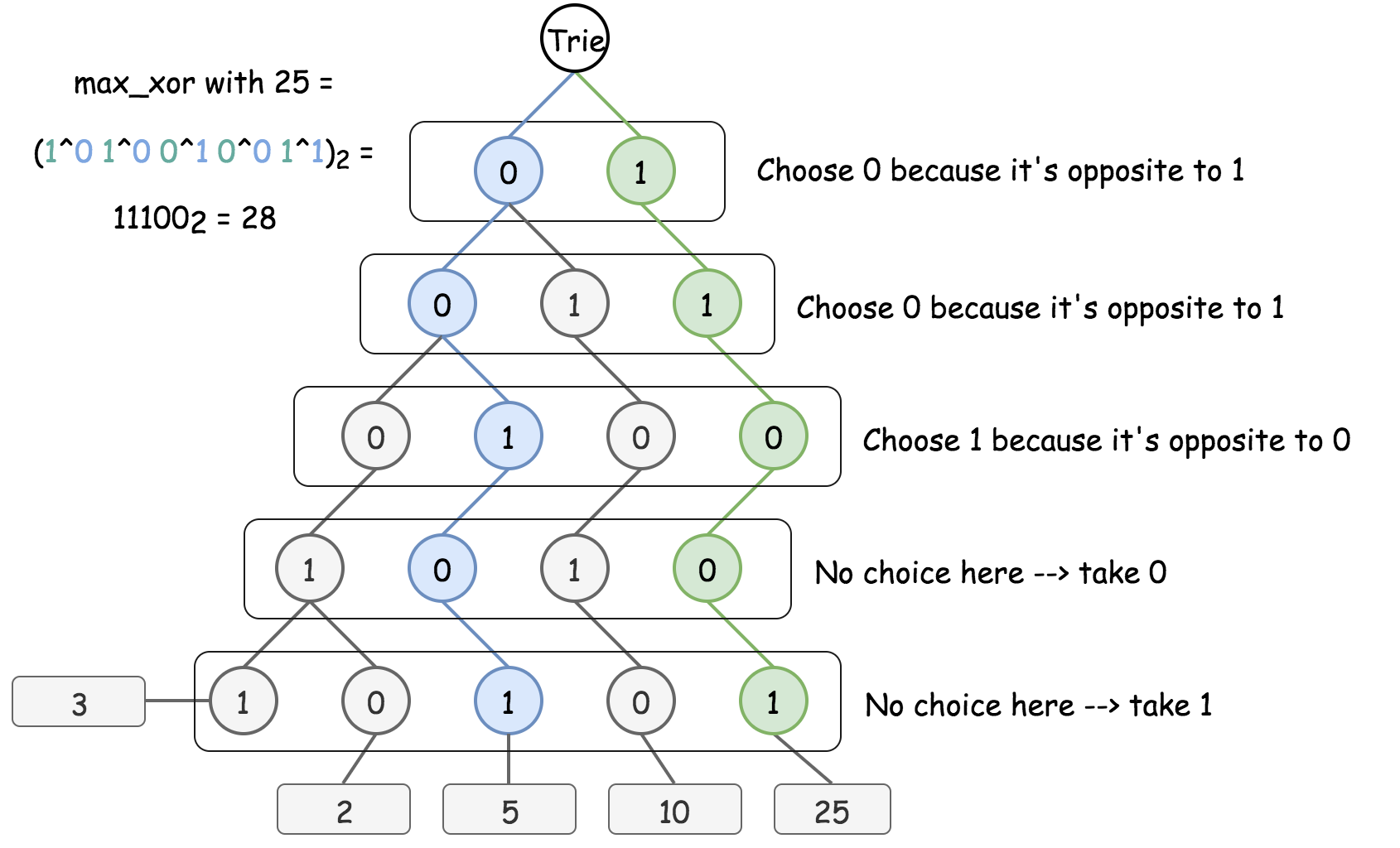
Time complexity: O(n). It takes O(L) to insert a number in Trie, and O(L) to find the max XOR of the given number with all already inserted one, where L is the length of max number in a binary representation and is considered as a constant.
Space complexity: O(1) extra space, since one needs O(2^L) space to keep Trie, which is considered constant.
class TrieNode {
public:
TrieNode(int alphabet_size) {
children = vector<TrieNode*>(alphabet_size);
}
~TrieNode() {
for (auto child : children)
delete child;
}
vector<TrieNode*> children;
};
class BitwiseTrie {
public:
BitwiseTrie() {
root = new TrieNode(2);
}
~BitwiseTrie() {
delete root;
}
void insert(const vector<int>& binaryNum) {
TrieNode* node = root;
for (int bit : binaryNum) {
if (!node->children[bit]) {
node->children[bit] = new TrieNode(2);
}
node = node->children[bit];
}
}
int maxXOR(const vector<int>& binaryNum) {
TrieNode* xorNode = root;
int maxXOR = 0;
for (int bit : binaryNum) {
int toggledBit = 1 - bit;
if (xorNode->children[toggledBit]) {
maxXOR = (maxXOR << 1) | 1;
xorNode = xorNode->children[toggledBit];
} else {
maxXOR = maxXOR << 1;
xorNode = xorNode->children[bit];
}
}
return maxXOR;
}
private:
TrieNode* root;
};
vector<int> toBinary(int n, int L) {
vector<int> res(L, 0);
int i = L - 1;
while (n > 0) {
res[i--] = n % 2;
n /= 2;
}
return res;
}
class Solution {
public:
int findMaximumXOR(vector<int>& nums) {
int maxNum = *max_element(nums.begin(), nums.end());
if (maxNum == 0)
return 0;
// find the length L of max number in a binary representation
int L = 0;
while (maxNum > 0) {
maxNum = maxNum >> 1;
L++;
}
BitwiseTrie trie;
int maxXOR = 0;
for (int num : nums) {
// convert num to binary representation
vector<int> binaryNum = toBinary(num, L);
// build bitwise trie
trie.insert(binaryNum);
// compute max xor for already inserted numbers
maxXOR = max(maxXOR, trie.maxXOR(binaryNum));
}
return maxXOR;
}
};